Neural Network for Solving Mathematical Expression
In this article, I propose a neural network (NN) for solving mathematical expression with or without paranthesis.
\[5 + 3 \times 2 + 1\]
\[(6 + 9) \times 3 + 7\]
\[[(3 + 2) \times 2] + 1\]
\[(3 \times 2 + 7) + 2\]
For simplicity, we'll limit the number of operands to four each \(\in \{1,2,3,4,5,6,7,8,9\}\) and use two operators, \(\in \{+, *\}\), only.
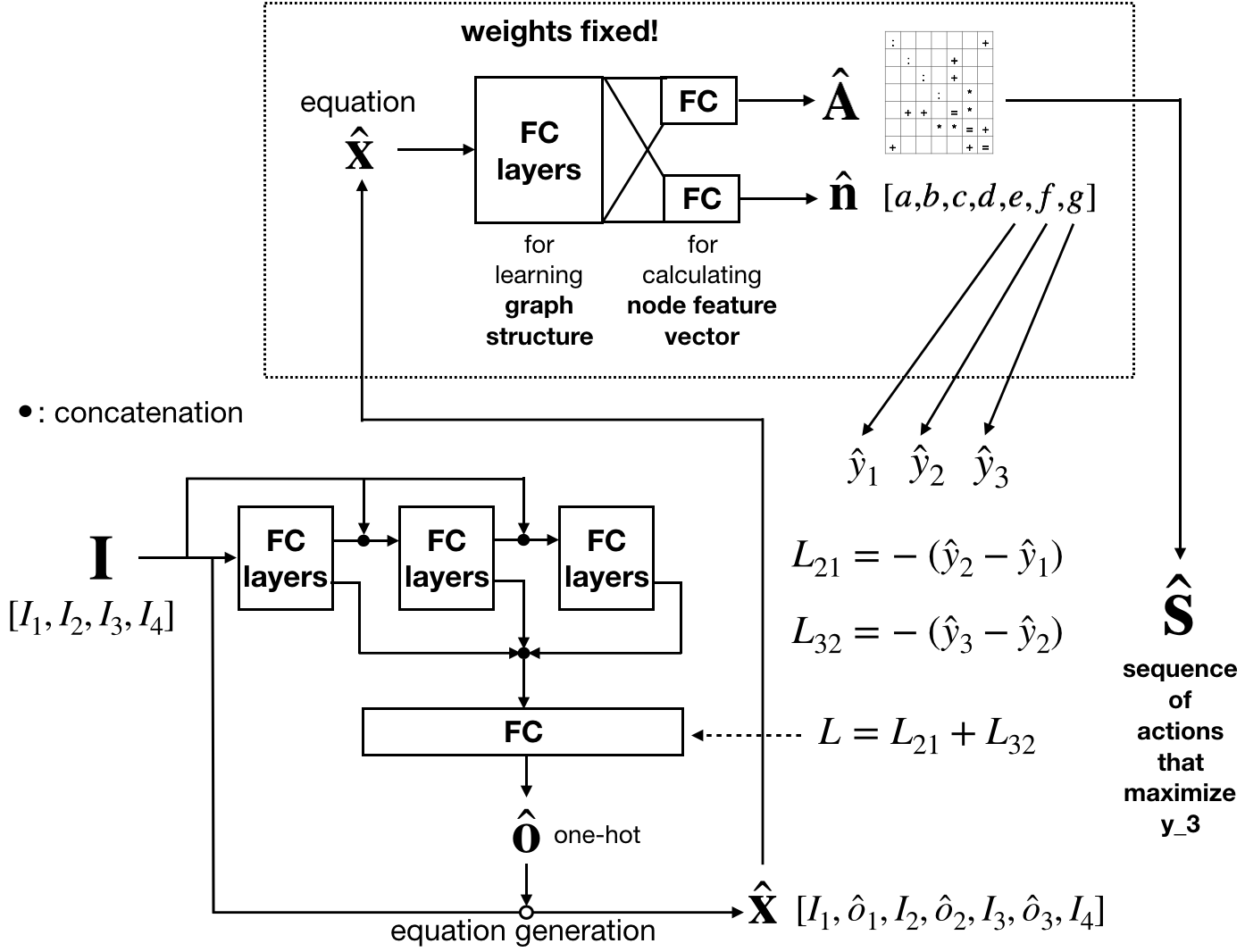
Typically mathematical expressions are expressed by a binary expression tree as shown in the left of the following figure. Notice that in a binary expression tree, internal nodes correspond to math operators and leaf nodes correspond to operands. However, another possible approach is shown in the right of the following figure. Notice that all nodes correspond to values (leaf nodes correspond to operands) and all edges correspond to operators. As we’ll discuss later, this design is to encode all values (including operands) as node features and all operators as edge features. Furthermore, operands are continuous real numbers while operators are discrete values.
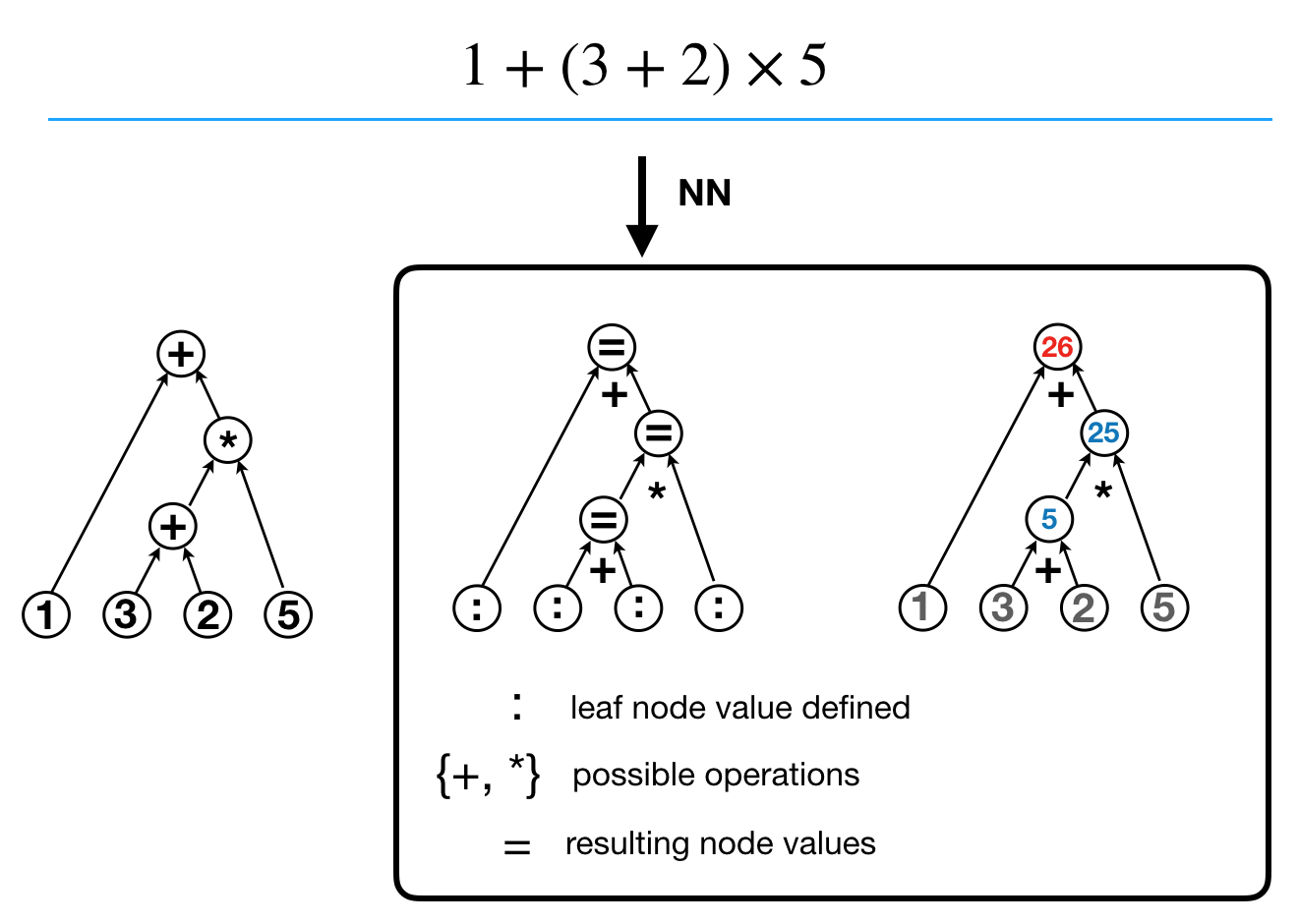
Computation tree of a mathematical expression can be represented using edge feature tensor and node feature vector as follows:
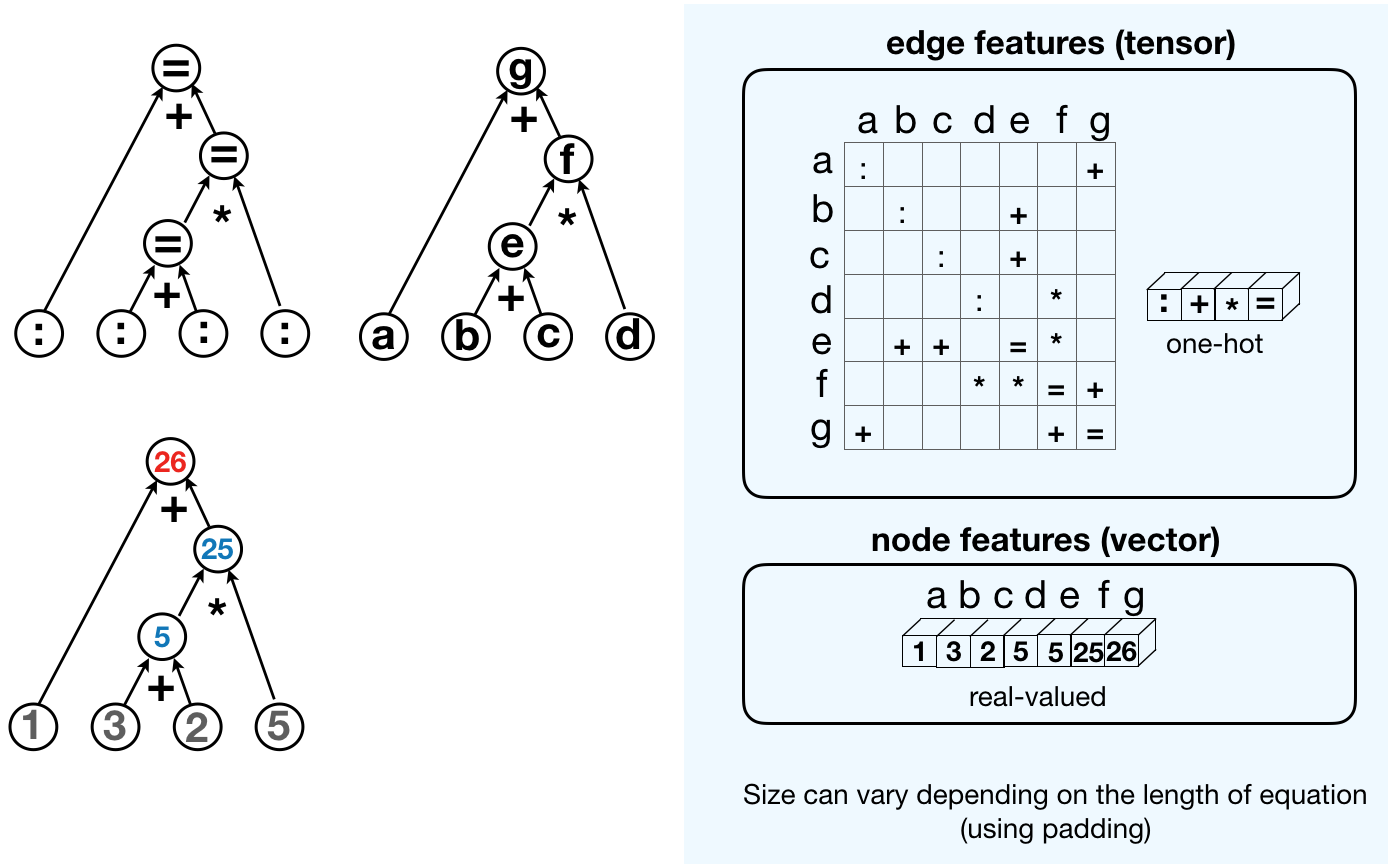
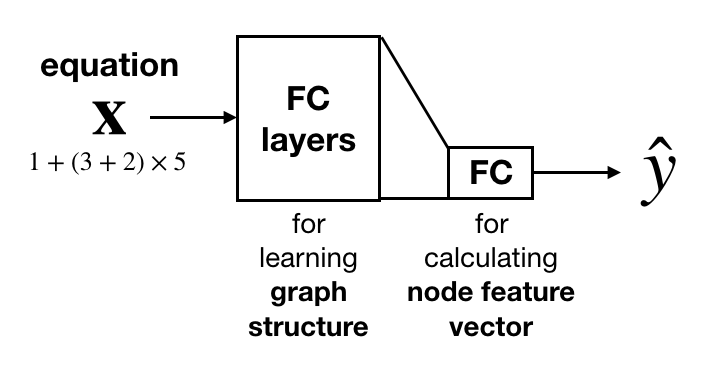
Hence the task of solving mathematical expression reduces to predicting edge feature tensor and node feature vector of corresponding computation tree. A possible NN architecture is shown below:
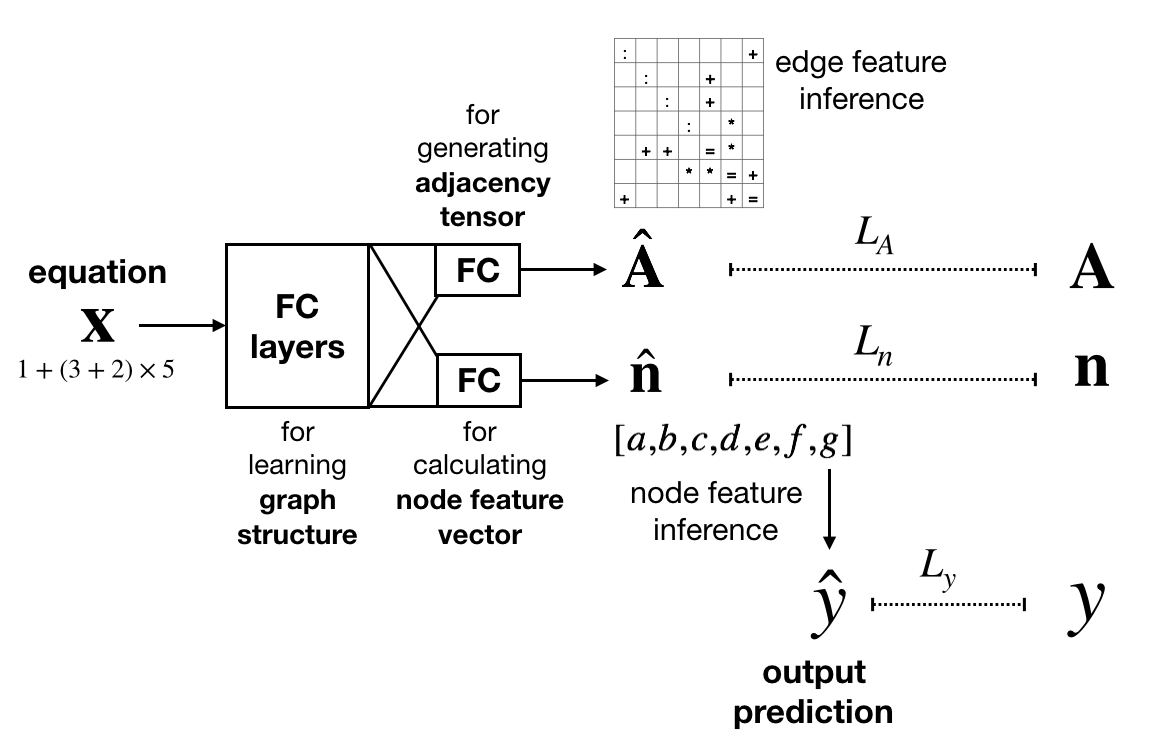
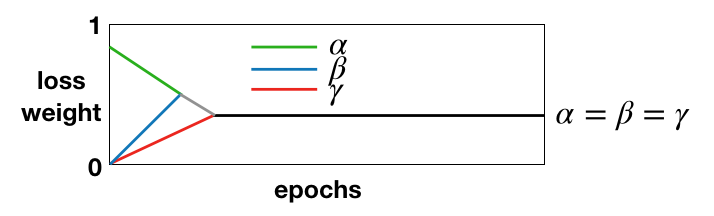
\(\boldsymbol{A}\) denotes edge feature tensor, \(\boldsymbol{n}\) denotes node feature vector, and \(y\) denotes the output of mathematical expression. We can use a weighted loss, \(L = \alpha L_A + \beta L_n + \gamma L_y\). The weight factor of edge feature tensor, \(\alpha\), is the highest when training begins such that the NN focuses on learning the computation tree; if the predicted edge feature tensor is invalid (e.g., not symmetric), then node feature vector is invalid by default. All three weight factors are annealed to 1/3 eventually.
During test time, we can simply use the fully connected layer that outputs the node feature vector to obtain \(\hat{y}\).
Additionally, this approach can be extended to develop a NN for determining the order of actions as exampled below:
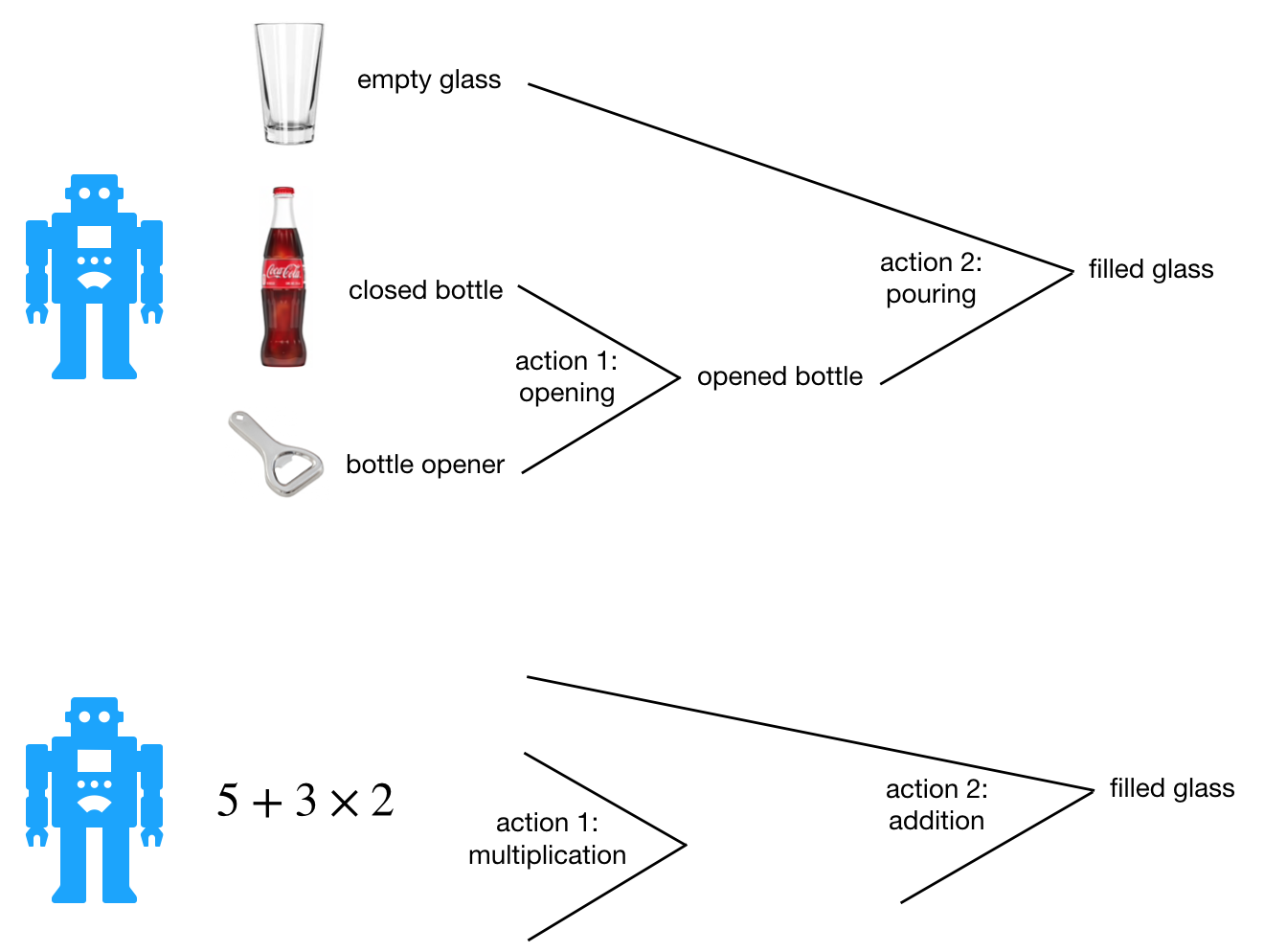
For simplicity, we’ll limit the number of objects to \(I \in \{ - 9,{\rm{ }} - 8,{\rm{ ..., }} - 1,{\rm{ 0, + 1, ..., }} + 9\}\) and the number of operations to \(O \in \{ + ,{\rm{ }} - ,{\rm{ }} \times {\rm{, }} \div \}\). The objective is that given four numbers (objects), generate the maximum output (reward) using 3 different operations. In other words, the task is to determine the order of actions that gives the maximum reward. Keep in mind the operator cannot be repeated, and parenthesis is not allowed.
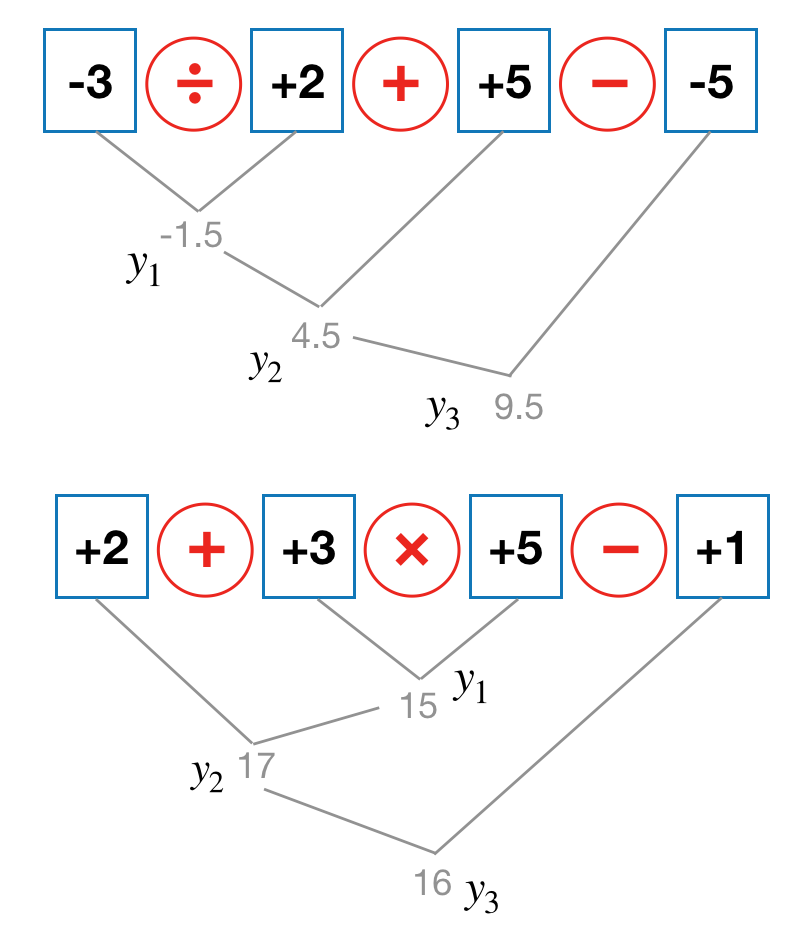
Lastly, we can use the following architecture to train the model: