Generalizable Neural Network for Learning Algebraic Operations Using Quantity Encoding and Abstract Representation of Numbers
Download:
PDFAbstract
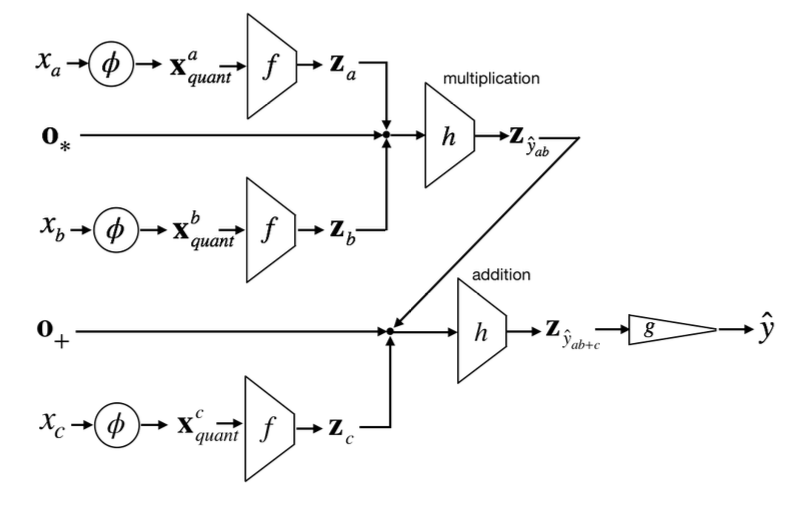
I propose a neural network, Q-Net, capable of generalizing basic math operations to unseen numbers. The key components of Q-Net are quantity encoding of numbers and abstract representation of quantities, which were inspired from children’s algebra learning process and autoencoder’s exploratory power of latent space. Q-Net is comprised of two modules: A- module and C-module. Numbers are first represented by quantity encodings and encoded numbers are fed into autoencoder-like A-module, where the encoder part of the A-module extracts the abstract representation of numbers. Algebraic operations are carried out by C- module using the learned abstract representation of numbers, and the abstract representation of resulting number is decoded to output number by the decoder part of A-module. Compare to baseline models, Q-Net showed significantly better performance for multiplication with unseen numbers.