EuNet: Artificial Neural Network with Feedback Connections
In my previous article, Towards the Next Generation of Artificial Neural Network, I suggested feedback connections in artificial neural network (ANN) to make ANNs closer to biological neural networks (BNNs) in human brain. In this article, I will briefly describe how feedback connections can be implemented. The resulting ANN architecture will be called the EuNet.
ResNet, which uses feedforward skip connections (left side of the figure), is an example of ANN that breaks the sequential nature of ANN architecture. A possible feedback connection (as a counterpart of ResNet block) is shown in the right side of the following figure.
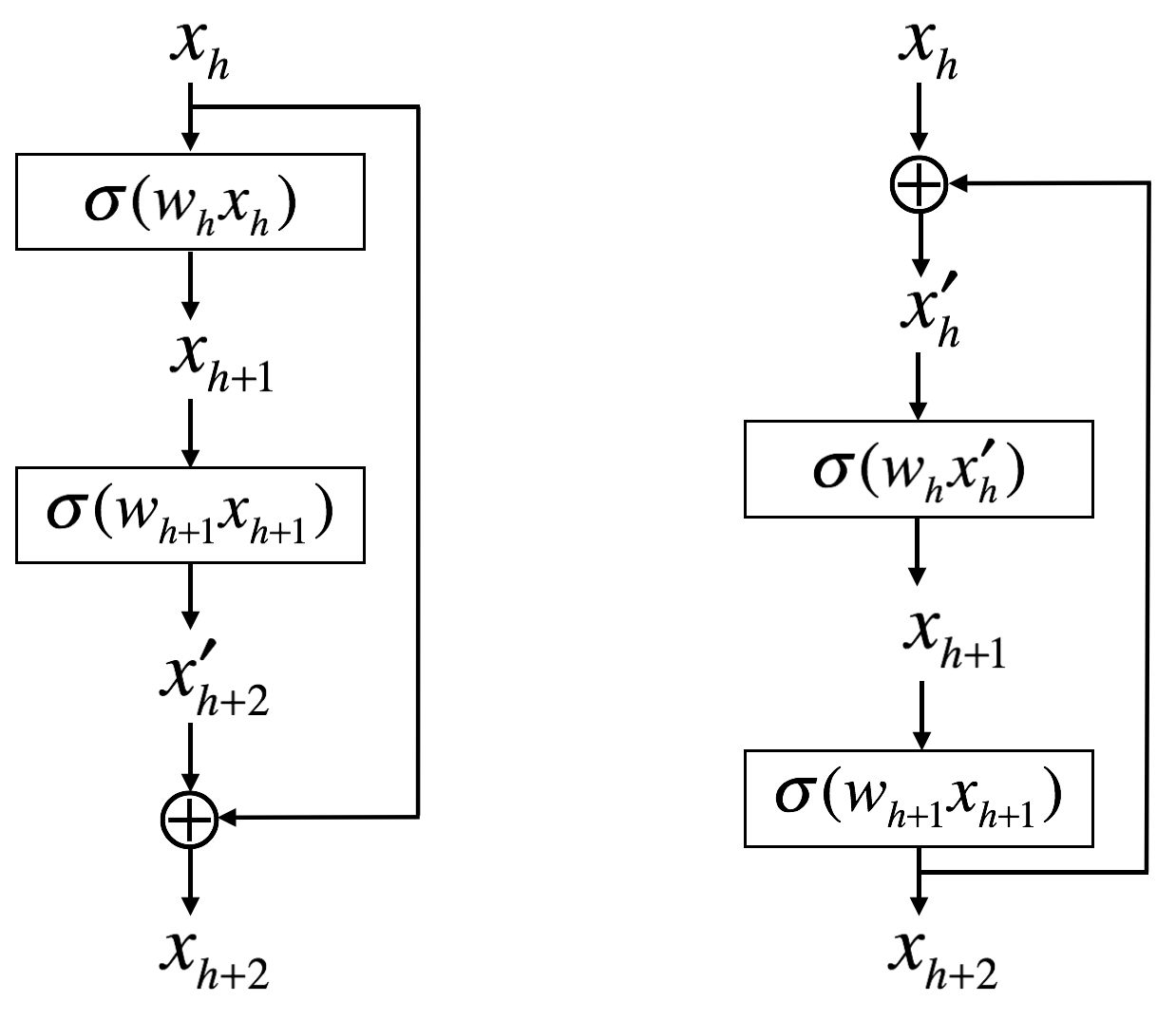
Note that feedforward as well as feedback connections do not need to be skip connections; they can directly connect input and output of a node. Thus, we can make a generalization as follows.
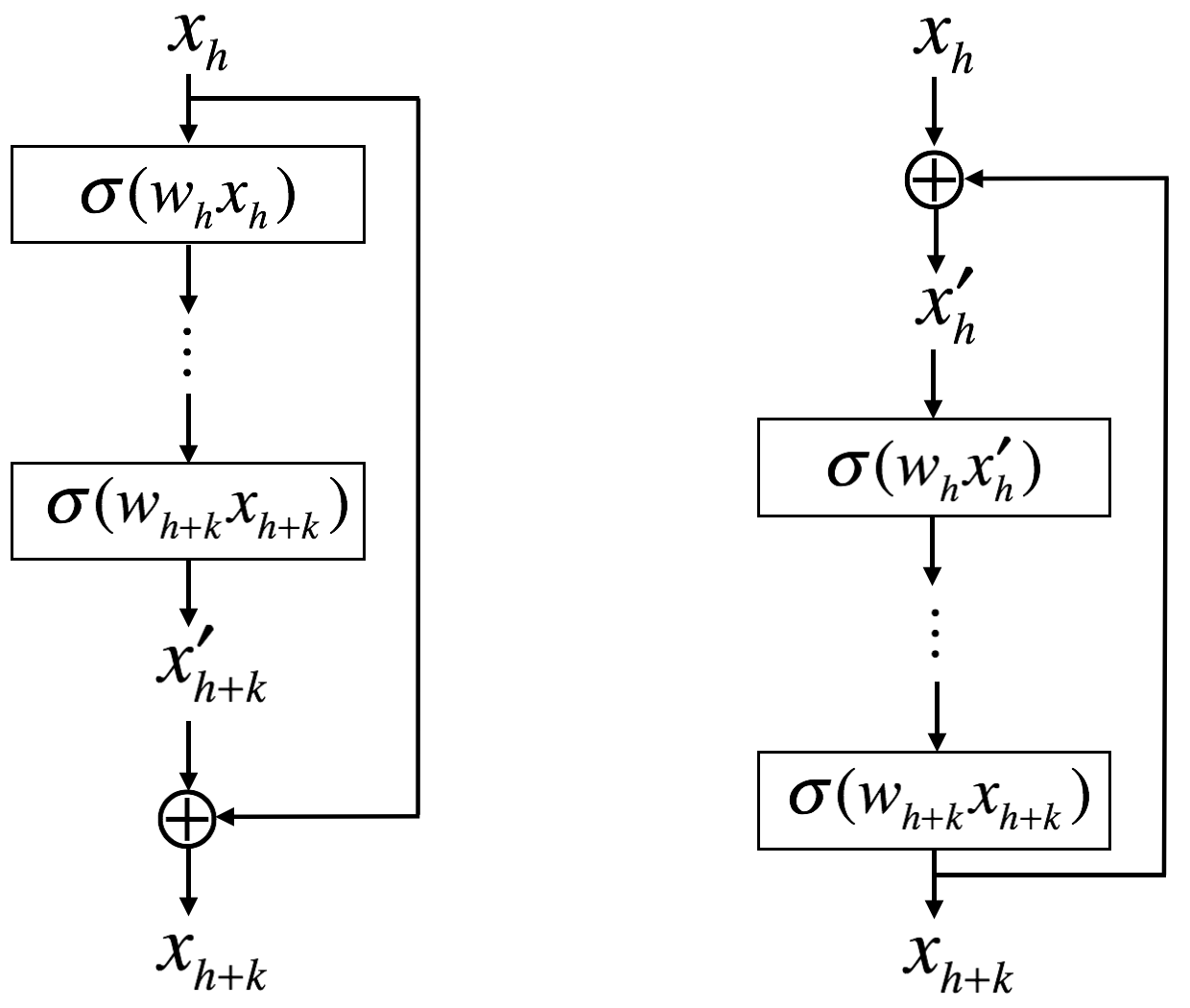
Feedforward skip connections can be easily implemented as follows.
\[\begin{aligned} x_h &= c \\ x_{h+1} &= \sigma(w_{h+1}x_h) \\ x_{h+2}^{'} &= \sigma(w_{h+2}x_{h+1})\\ x_{h+2} &= x_{h+2}^{'} + x_{h+1} \end{aligned}\]
However, there is a serious problem for the feedback connections.
\[\begin{aligned} x_h &= c \\ x_h^{'} &= x_h + x_{h+2} \\ x_{h+1} &= \sigma(w_{h+1}x_h^{'}) \\ x_{h+2} &= \sigma(w_{h+2}x_{h+1})\\ \end{aligned}\]
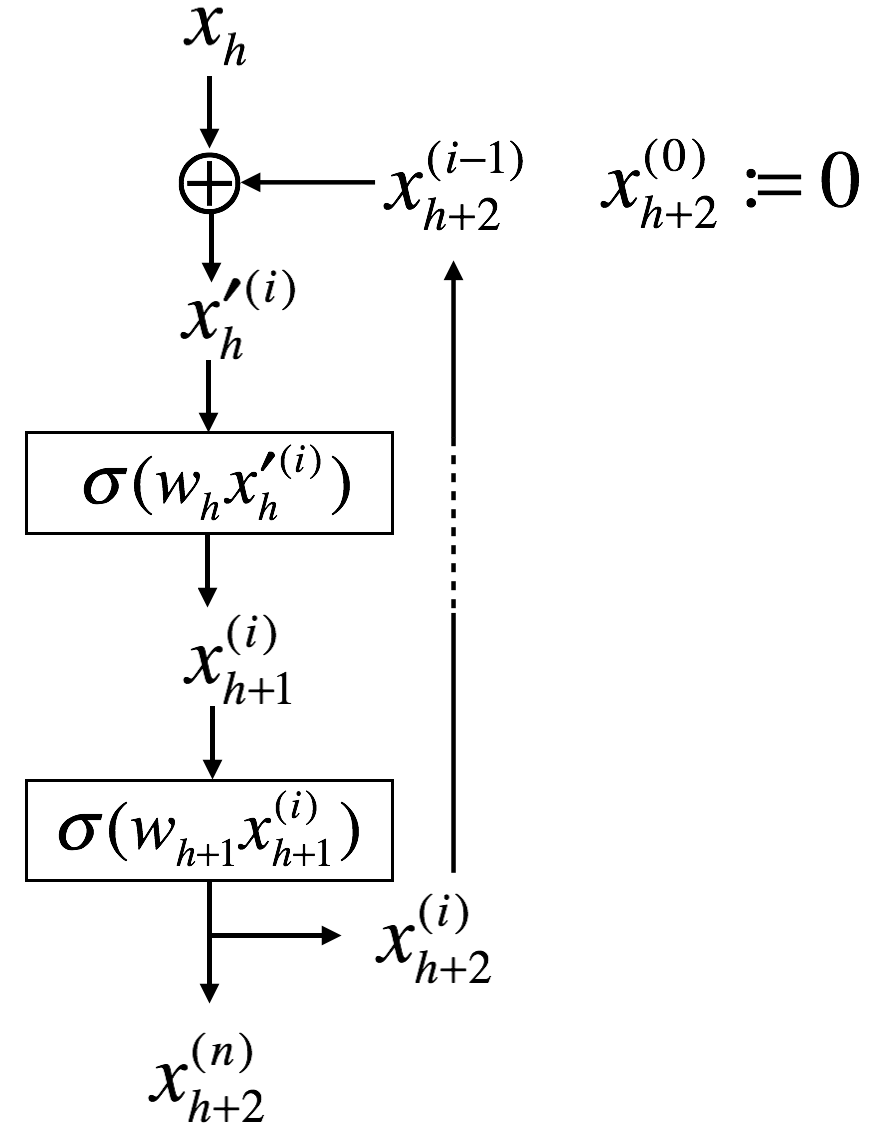
But \(x_{h+2}\) is required to obtain \(x_h^{'}\) before \(x_{h+2}\) is defined. Thus, the above equations cannot be implemented. One solution is to use a loop as shown in the following figure.
import numpy as np
def logistic_func(x):
y = 1 / (1 + np.exp(-x))
return y
def loop(x_in, w_1, w_2):
outputs = [ ]
for i in range(25):
if i == 0:
x_0 = x_in
else:
x_0 = x_in + x_2
x_1 = logistic_func(w_1 * x_0)
x_2 = logistic_func(w_2 * x_1)
print(x_2)
outputs.append(x_2)
return outputs
As long as a sigmoidal function (e.g., logistic function or tanh function) is used as an activation function, the output of the loop will always be bounded; on the other hand, the output has no bound if ReLU or LeakyReLU is used (I talk about why I think of activation functions that have no bounds (e.g., ReLU, LeakyReLU) as ad hoc solutions to the state-of-the-art deep learning in my previous article ). However, ANN becomes inefficient if such loops are used for every feedback connections. Moreover, we need to develop a way for loss backpropagation through the loops.
A possible solution I would like to suggest is to use training epochs as the iterations of the loop. At the first epoch (\(i=0\)), \(x_h^{'(0)}\) are calculated without feedback connections and weights are updated by loss backpropagation as usual. Then, for \(i \ge 1\), \(x_h^{'(i)}\) are calculated with feedback connections (e.g., \(x_h^{'(i)} = x_h^{(i)} + x_k^{'(i-1)}, k>h>1\)).
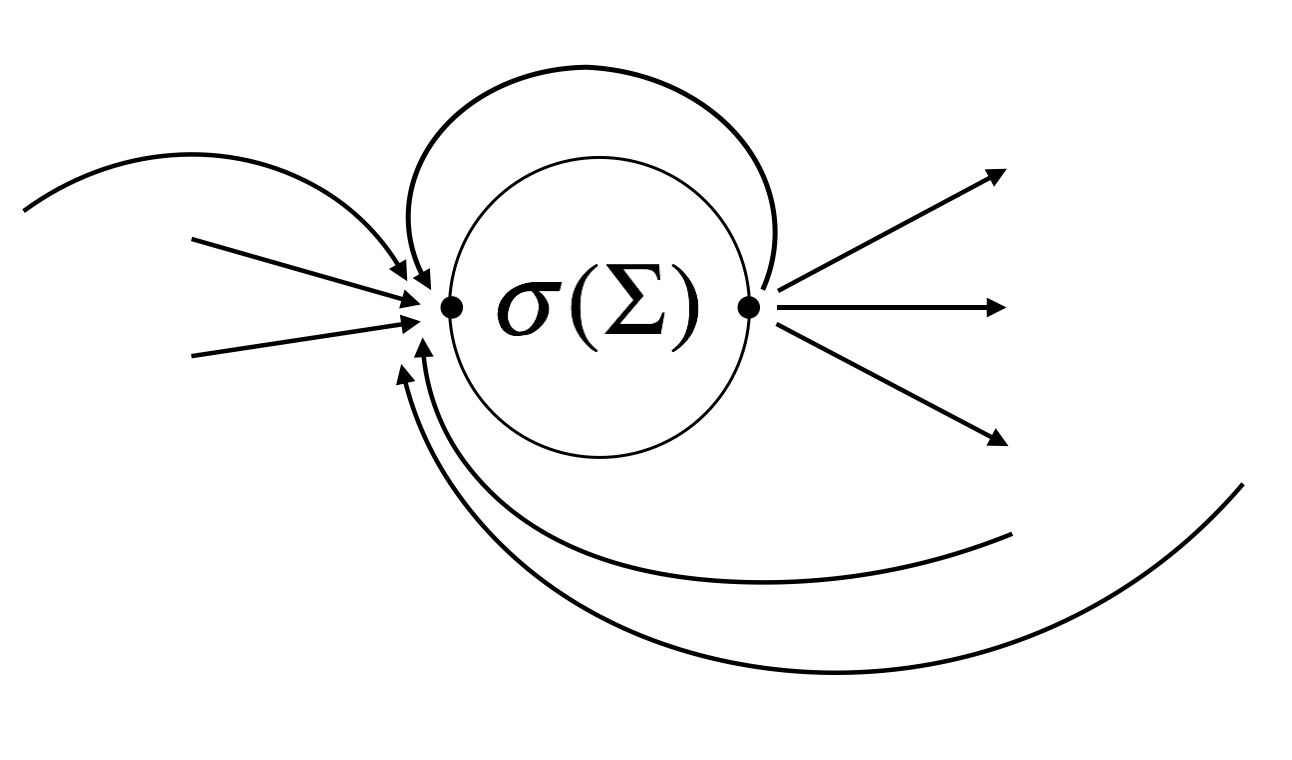
Now, think of a gate that regulates the connectivity of skip connection as follows (\(g\) is a learnable weight).
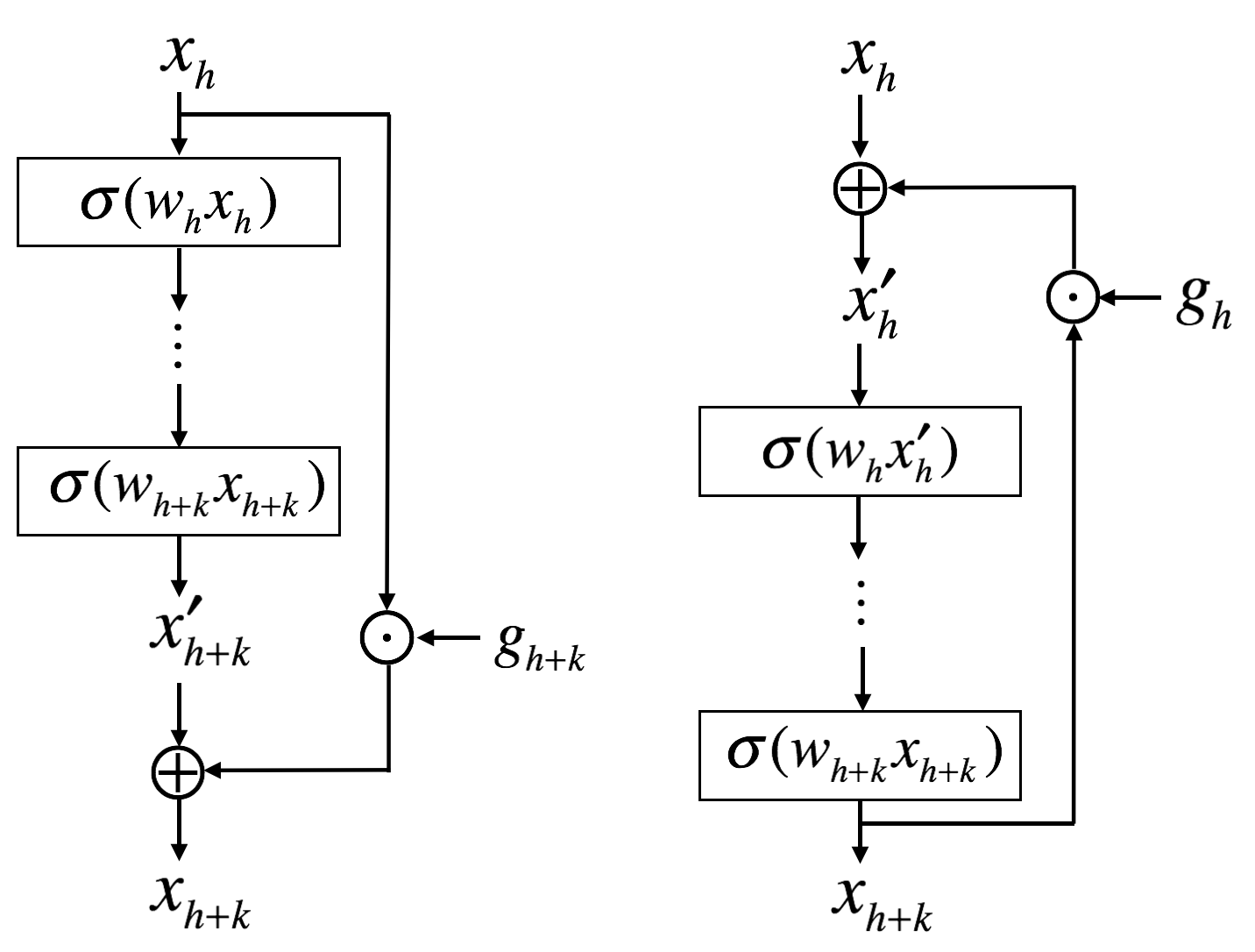
Then, consider all possible feedforward connections as well as feedback connections as shown in the following figure.
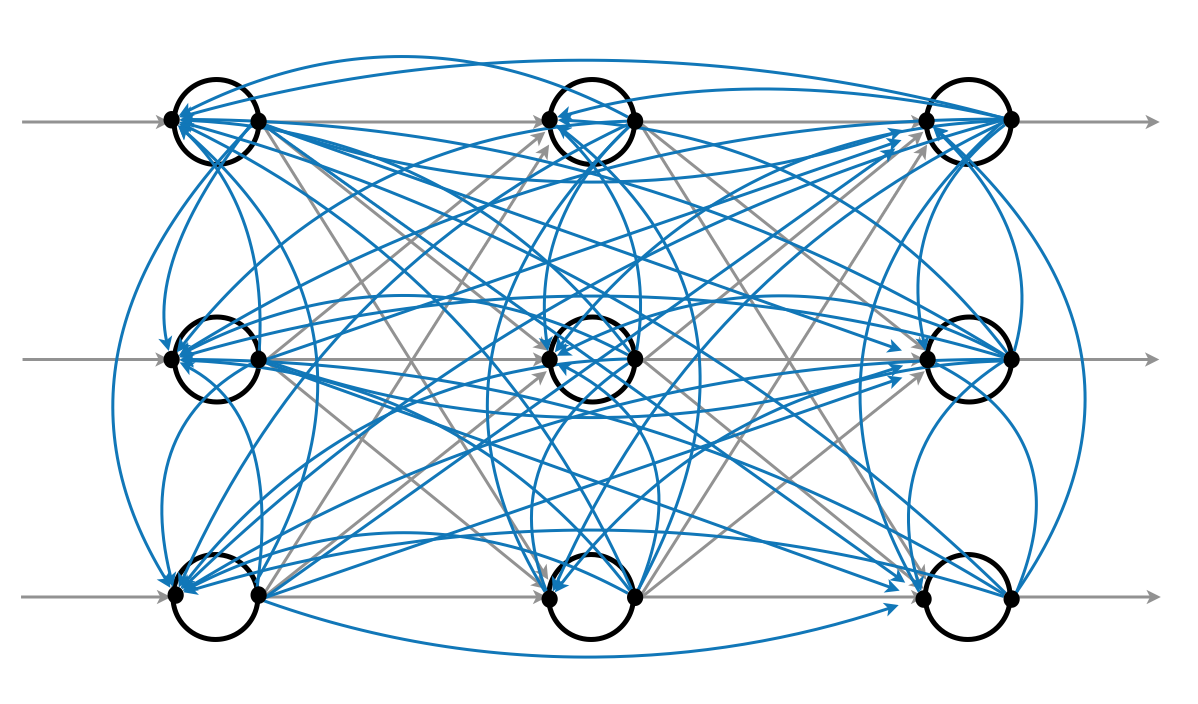
In conventional neural network, a node takes a weighted sum of the outputs of the preceding nodes (\(\sum = \mathbf{Wx}\)). However, the node in the above architecture can take outputs of any other nodes (even including the node itself).
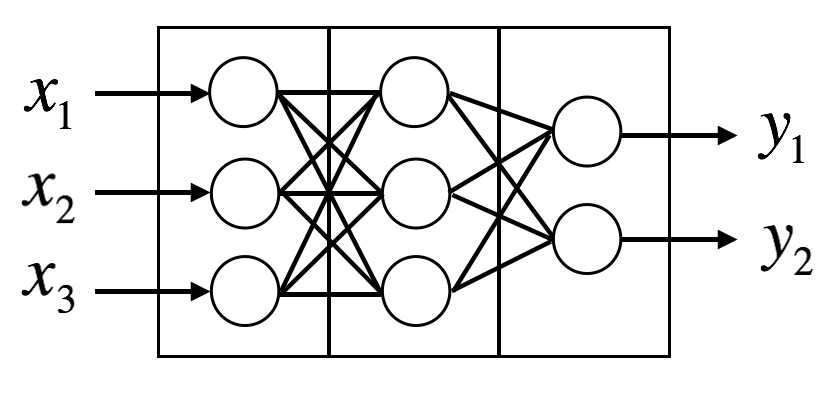
To construct and train such neural network with nodes as shown above, first construct a multi-layer perceptron without skip connections as follows.
At epoch \(i=0\), outputs of nodes are calculated for each layer \(h\).
\[\mathbf{x_{h+1}}^{(0)} = \sigma(\mathbf{W_h}^{(0)}\mathbf{x_h}^{(0)})\]
and define a a vector containing all outputs of nodes.
\[x_{\text{all}}^{(0)} = \begin{bmatrix} x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_N^{(0)} \\ \end{bmatrix}\]
Then, all weights are updated using backpropagation. For \(i \ge 1\), calculate the outputs of layer \(h\) with \(k\) nodes as follows:
\[\begin{aligned} \mathbf{X}_h^{*(i)} &= \begin{bmatrix} g_{h, 11}^{(i)} & g_{h, 21}^{(i)} & \ldots & g_{h, N1}^{(i)} \\ g_{h, 12}^{(i)} & g_{h, 22}^{(i)} & \ldots & g_{h, N2}^{(i)} \\ \vdots & \vdots & \ddots & \vdots \\ g_{h, 1k}^{(i)} & g_{h, 2k}^{(i)} & \ldots & g_{h, Nk}^{(i)} \end{bmatrix} \mathbf{x}_{\text{all}}^{(i-1)} \\ &= \mathbf{G}_h^{(i)}\mathbf{x}_{\text{all}}^{(i-1)} \\ \mathbf{x}_h^{'(i)} &= \mathbf{W}_h^{(i)} \mathbf{x}_h^{(i)} + \mathbf{G}_h^{(i)} \mathbf{x}_{\text{all}}^{(i-1)} \\ \mathbf{x}_{h+1}^{(i)} &= \sigma(\mathbf{x}_h^{'(i)}) \end{aligned}\]
Then, the sets of weights \(\mathbf{W}^{(i)}\) and \(\mathbf{G}^{(i)}\) can be updated using backpropagation. Summarized architecture is as follows:
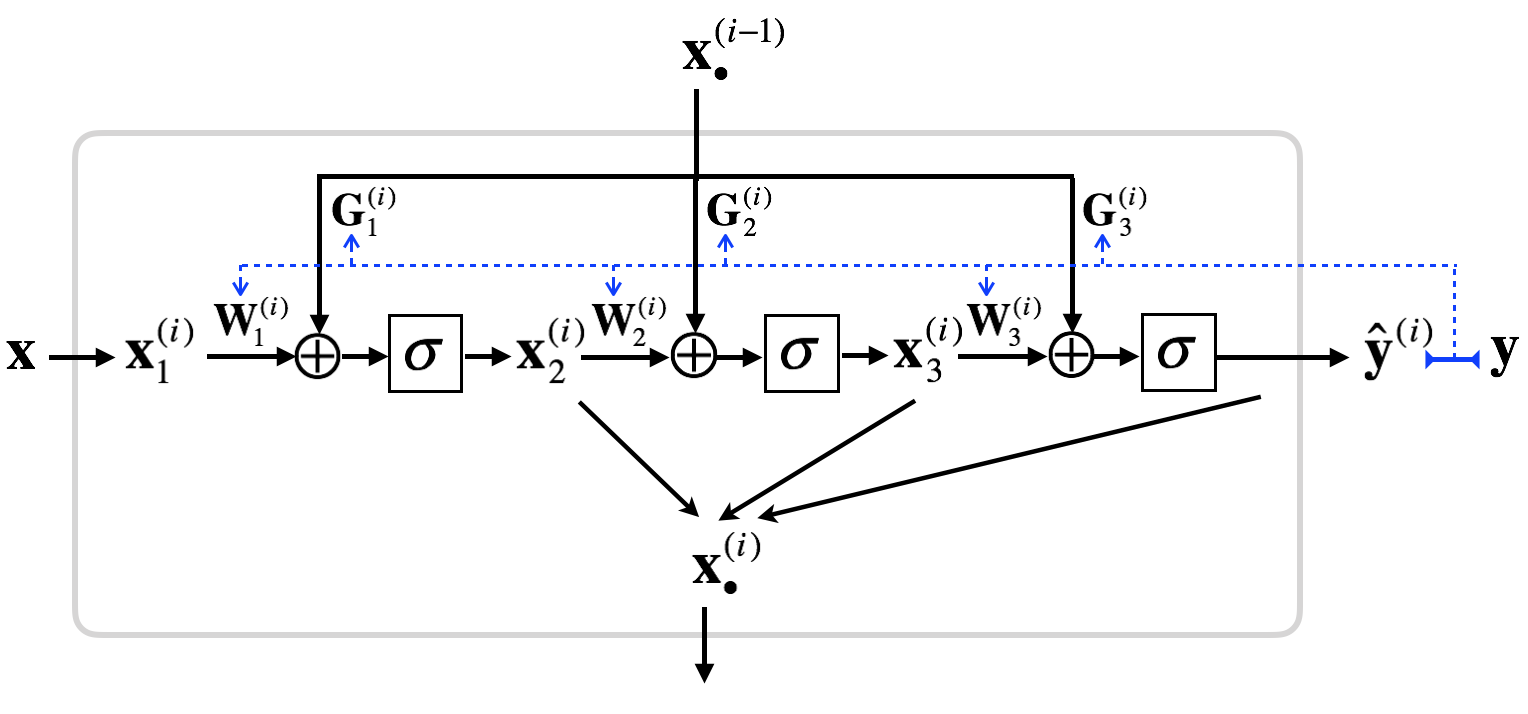
Note that the neural network becomes MLP if all gate weights (\(\mathbf{G}_h\)) are zero. And all nodes are inter-connected through \(\mathbf{G}_h \mathbf{x}_{\text{all}}\), although they appeare disconnected at the moment \(i\). Thus, learning the gate weights \(\mathbf{G}_h\) is equivalent to learning the architecture of neural network. I will call the neural network suggested ’EuNet.’ I think that EuNet is a generalization of all possible ANN architectures. For example, convolutional neural network and recurrent neural network can be viewed as a special case of EuNet.
I did a simple experiment as proof of concept that EuNet is capable of memorizing sequential data.
Listen to the piano notes of the original song, You are My Sunshine, used to train models:
Listen to the piano notes memorized by MLP:
Listen to the piano notes memorized by Feedback Model:
Listen to the piano notes memorized by EuNet:
Listen to the piano notes memorized by LSTM:
Code available at https://github.com/minjeancho/EuNet